
こんな悩みにお答えします。
1. Aidemy
・・・AIエンジニアとしてのスキルを身に付けたい。その延長で就職、転職できたら嬉しい方におすすめ。
2.侍エンジニア塾
・・・基礎力と即戦力を身に付けられる、満足度No.1スクール
3. TechAcademy
・・・副業に向けてスキルアップしたい。フリーランスなどを目指している方向け。
4. AIジョブカレッジ
・・・コスパ良く、質の高い講座を受けたい方におすすめ。
本記事の信頼性

現在はデータサイエンティストとして大企業で活動しています。

ProphetはPythonで利用することができる
時系列データの解析方法はいくつかありますが、Prophetでは時系列データを3つの項の和として回帰モデルを構築しています。
$$y(t)=g(t)+s(t)+h(t)+\varepsilon_t$$
上の式から分かる通り、Prophetは自己回帰のように過去の結果を基に未来を予測しているわけではありません。データをプロットしたときに上手くデータを通るような曲線を引いているだけのシンプルなモデルです。
故に欠損値の補完などの前処理も不要で、データを時間カラムdsと目的変数カラムyに整形しProphetに渡してあげるだけで簡単に予測を行うことができます。
・
以降、実際にコーディングしていく上で、実行環境を記載いたします。
- Python:3.6.4
- fbprophet:0.7.1
- pandas_datareader:0.10.0
まずはインストールから実施していきます。Prophetはpipによりインストールすることができます。
$pip install fbprophetただ、ここでエラーが出る方が非常に多いそうです。調べるといくつか解法が載っていますが、私は仮想環境上で実行し問題なくインストールできました(仮想環境の構築は以下を参照ください)。
>>【Python】Windows10へのインストール方法を解説(スクリーンショットあり)
>>【Python】【初心者必見】仮想環境の構築~venvの設定方法~
また、今回は株価の予測を行うため、株価を取得できるライブラリもインストールしておきましょう。
$pip install pandas_datareader>>【Python】初心者必見の株価取得方法~ライブラリ利用~

これで準備はOK!Prophetによる株価予測を体験してみましょう。
4. Prophetによる株価予測
ここから、米国株の有名指標であるS&P500を対象としProphetを用いた株価予測を行っていきます。
a. 実験設定
以下の条件の下株価予測を行う。
| 対象 | S&P500 |
| 期間 | 2016/1/1~2022/4/30(取得期間) 2016/1/1~2022/3/31(学習) 2022/4/1~2022/5/31(予測) 2022/4/1~2022/4/30(テスト) |
| モデル | Prophet(①株価、②株価対数) |
| パラメータ | デフォルト |
2022年3月までのデータを基にモデルの学習を行い、4~5月の株価を予測します。予測結果が正しいかの確認を4月分の実データと比較していきます。
また、株価のモデリングには対数が用いられる場合が多いです。したがって、株価をそのまま利用したケースと株価の対数を取ったケースの2パターン実施します。
また、Prophetには複数のパラメータが存在しますが、今回は簡単のためデフォルト値をそのまま利用しています。
| パラメータ | 説明 | デフォルト |
まずは、pandas-datareaderを用いて株価を取得します。
import pandas_datareader.data as web
#期間指定
st = '2016/01/01'
ed = '2022/05/01'
st_train = '2016/01/01'
ed_train = '2022/03/31'
st_test = ed_train
ed_test = '2022/04/30'
#期間を指定し、S&P500(^GSPC)の株価を取得
stooq = web.DataReader(['^GSPC'], 'yahoo',start=st,end=ed)これにより、S&P500の以下の情報を取得することができます。この中で「Date」と「Adj Close」を用いてモデリングを行います。
| カラム名 | 意味 |
| Date | 日付 |
| High | 高値 |
| Low | 安値 |
| Open | 始値 |
| Close | 終値 |
| Volume | 出来高 |
| Adj Close | (調整後)終値 |
Prophetが読み込めるように取得したデータを整形します。
import numpy as np
#####################学習データ
df = stooq[st_train:ed_train]
df = df.dropna(how='any')
#対数変換する場合
#df['Adj Close'] = np.log(df['Adj Close'])
df = df.reset_index()
df[['ds','y']] = df[['Date' ,'Adj Close']] #カラム名を変更
df = df[['ds','y']] #余分なカラムを削除
#####################テスト(正解)データ
df_actual = stooq[st_test:ed_test]
df_actual = df_actual.dropna(how='any')
#対数変換する場合
#df_actual ['Adj Close'] = np.log(df_actual ['Adj Close'])
df_actual = df_actual .reset_index()
df_actual [['ds','y']] = df_actual [['Date' ,'Adj Close']] #カラム名を変更
df_actual = df_actual [['ds','y']] #余分なカラムを削除
#####################オリジナルデータ(学習データ+テストデータ)(可視化用)
stooq = stooq.dropna(how='any')
#対数変換する場合
#stooq['Adj Close'] = np.log(stooq['Adj Close'])
stooq = stooq.reset_index()
stooq[['ds','y']] = stooq[['Date' ,'Adj Close']] #カラム名を変更
stooq = stooq[['ds','y']] #余分なカラムを削除
時間カラムを「ds」、目的変数カラムを「y」とすることに注意してください!
また、冗長な箇所がございますので必要に応じて修正してご利用ください。
いよいよProphetを用いた学習・予測フェーズです。
from fbprophet import Prophet
period = 61 #予測日数(4~5月)
m = Prophet()
m.fit(df) #学習データでモデリング
future = m.make_future_dataframe(periods=period)
forecast = m.predict(future) #予測結果
####可視化(予測結果)
plt.rcParams["font.size"] = "25"
fig, ax = plt.subplots(figsize=(20,10))
pd.plotting.register_matplotlib_converters()
m.plot(forecast,ax=ax);
ax.plot(stooq["ds"],stooq["y"],color="r")
plt.rcParams["font.size"] = "13.3"
ax.set_title('^GSPC')
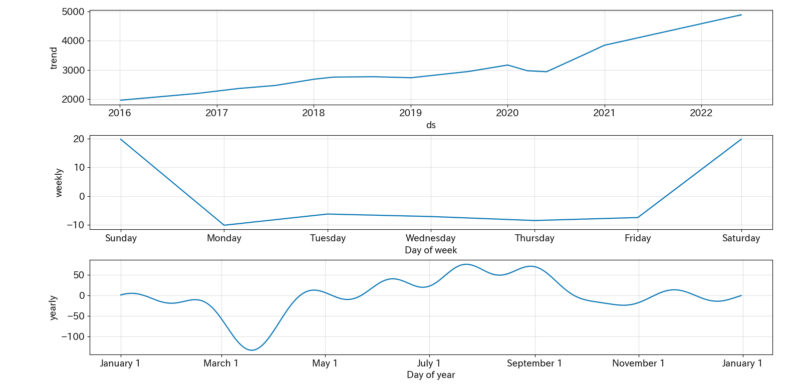
####可視化(トレンド、周期性)
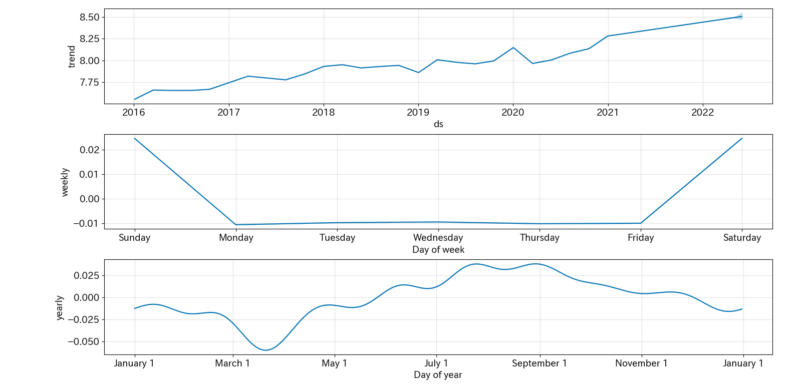
m.plot_components(forecast);上記コードから分かるように、学習から予測まで約5行程度で実装することができます。これがProphetの魅力ですね。
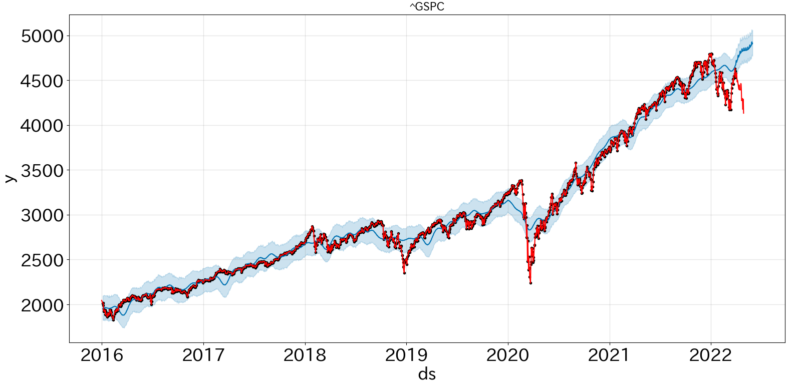
予測値の可視化結果は以下のとおりです。青が予測結果、赤が実測値(黒プロットは実測値兼学習データ)です。
①株価
②株価対数
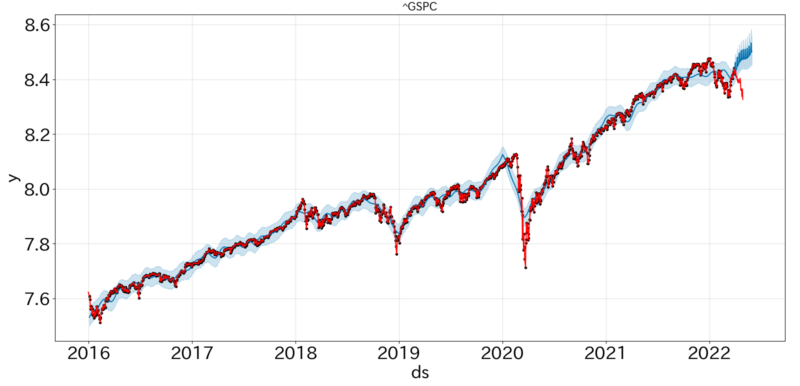
実験を行った期間は、金利上昇懸念に伴う下落市場であり予測が難しい期間となってしまいました。ただ、学習データについてはしっかりと追従することができています。そして、②対数株価の方が実測値との誤差が小さいように見受けられます。
学習期間では米国市場は好調であったこともあり上昇トレンドが見て取れます。また、3~4月にかけて下落傾向にあることも確認できます。これは、決算時期と重なっているため業績が芳しくなかった企業の株が売られているためと予想されます。
e. 評価
最後に、予測した株価の評価を行います。
ここでは、以下の方法で評価を行います。
- RMSLE (Root Mean Squared Logarithmic Error):外れ値に強く株価予測のコンペの評価指標としても有名。
- Prophetの予測範囲の中に実測値が含まれているデータ数
RMSLEの評価式は以下のとおりです。
$$RMSLE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(\log(y_i+1)-\log(\hat{y}_i+1))^2}}$$
from sklearn.metrics import mean_squared_log_error
stooq.columns = stooq.columns.droplevel(1)
ans = pd.merge(forecast, stooq, on="ds", how='inner')
ans.set_index("ds",inplace=True)
##########RMSLE
y_pred = ans[st_test:ed_test]["yhat"]
y_true = ans[st_test:ed_test]["y"]
#対数変換した場合
#y_pred = np.exp(y_pred)
#y_true = np.exp(y_true)
RMSLE=np.sqrt(mean_squared_log_error (y_true, y_pred))
print("RMSLE:",RMSLE)
##########予測範囲に入っているかどうか
y_pred_lower = ans[st_test:ed_test]["yhat_lower"]
y_pred_upper = ans[st_test:ed_test]["yhat_upper"]
ans_judge = ans[st_test:ed_test].copy()
#対数変換した場合
#y_pred_lower = np.exp(y_pred_lower)
#y_pred_upper = np.exp(y_pred_upper)
cnt = 0
for i in ans_judge.index:
if y_pred_lower[str(i)] <= y_true[str(i)] <= y_pred_upper[str(i)]:
cnt += 1
print("予測数:",len(ans_judge.index),"範囲内:",cnt)
評価結果は以下のとおりです。
| RMSLE | 予測範囲内のデータ数 (予測データ数:21) | |
| ①株価 | ||
| ②株価対数 | 6(28.6%) |
②株価対数の評価結果が良く、誤差が小さいことが確認されます。また、予測が難しい中でも約30%は予測範囲内に実測値が含まれている結果となりました。
対数を取りボラティリティを抑えることの大切さが分かりますね。
5. まとめ

今回は、しました。
Prophetを利用することで、たった数行のコーディングで株価の予測を行うことができました。また、株価の対数を取ることで精度の高い予測を実現できました。
今回は、Prophetのパラメータをすべてデフォルト値のまま使用しましたが、トレンドの転換点としてファンダメンタルズ分析の要素も取り入れることで更なる評価向上が期待できると思います。
Prophetは、Pythonで行う株価予測の第一歩としては最適な教材になるのではないでしょうか。ぜひあなただけのモデルを作成してみてください。
・【株式投資】Pythonでスクリーニングする方法
・【Python】【株式投資】TA-Libによるテクニカル指標算出方法(移動平均、ボリンジャーバンド、MACD、RSI)
・【初心者向け】20分でできる!Pythonで銘柄スクリーニング結果をスマホへ通知する方法
・【Python】銘柄スクリーニング結果を定期的に通知する方法(無料)【30分でできる!】
本ブログでは、株式やプログラミングに関する記事を投稿しています。
プログラミング(Python)を学びたい方におすすめの書籍やプログラミングスクール、おすすめの学習方法などをご紹介しておりますのでぜひご覧ください。
は、プログラミングスクールという方法がおすすめです。
私の一押しは『TechAcademy』です。
質問することですぐに分からないところをクリアにできますし、進捗をサポートしてくれるため確実に成長することができます。
無料相談を実施しているため、まずは話を聞いてあなたのスタイルに合っているかどうか確認してみるのが良いと思います。







コメント